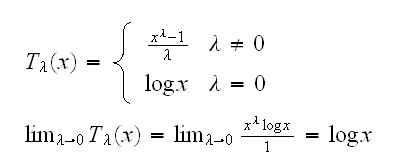
so we have a continuity of transforms. Special cases are 1/x, √x, xk (up to constants) etc.
Box & Cox in 1964 suggested a transformation of the form
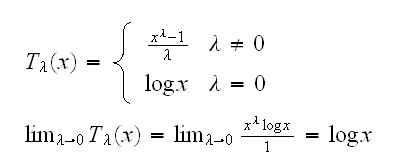
so we have a continuity of transforms. Special cases are 1/x, √x, xk (up to constants) etc.
There have been many suggestions for other transforms since then, but the Box & Cox power transform is still the most commonly used. The main question of course is how to choose λ, that is what value of λ makes Tλ(x) the most normal? There are two main approaches to this, maximum likelihood and Bayesian statistics. We will discuss the max likelihood approach here.
First we need a probability model. Say we are considering a simple linear regression problem, that is y=a+bx+E where E is a rv with some distribution. We want to transform the response y such that Tλ(y)~a-bx+N(0,σ). So our model has 4 parameters:(λ,a,b,σ). Of these it is λ we are after, without any special interest in a, b and σ (at this point). They are therefore nuisance parameters.
We want to do inference for λ, specifically we want to find a confidence interval. The standard approach for this is to find a corresponding hypothesis test, and invert the test. Here this is to test H0: λ=λ0; vs Ha: λ≠λ0. The usual first try to find a test would be the likelihood ratio test based on the test statistic
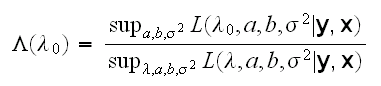
where in the numerator we fix λ at λ0, then find the maximum over a, b and σ2, and in the denominator we find the maximum over all four. But these are of course is the usual maximum likelihood estimates! Statistics theory then says that under some regularity conditions -2logΛ~Χ2(1).
What is L? It is the likelihood function of the transformed data. Now let Jλ(y) be the Jacobian of the transform from y to Tλ(y), then
Jλ(y) = d/dyTλ(y) = yλ-1
and so
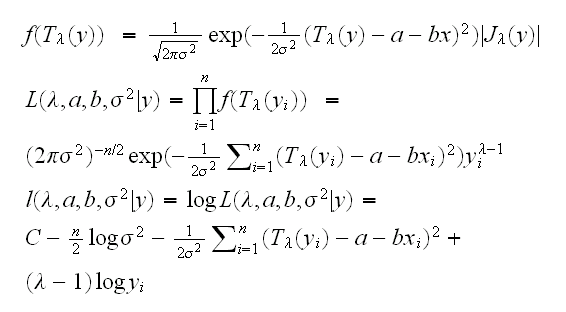
Now to find the numerator we fix λ at λ0 and find the maxima for a,b and σ2. This is done by taking derivatives, but then the last term vanishes, and we are left with the terms in a standard simple linear regression problem. Therefore we find
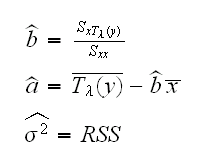
the standard estimates in a linear regression of Tλ(y) on x. So
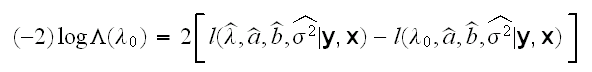
How do we find the mle of λ? We could try to do this analytically but this is not necessary, especially because we are trying to find a CI for λ anyway.
All this is implemented in boxcox.ex
There is a whole list of "transformation systems":
