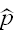 =X̄, the sample mean. By the Central Limit Theorem X̄~N(p,√(pq/n)), so a 100(1-α)% confidence interval for p is given by
=X̄, the sample mean. By the Central Limit Theorem X̄~N(p,√(pq/n)), so a 100(1-α)% confidence interval for p is given by 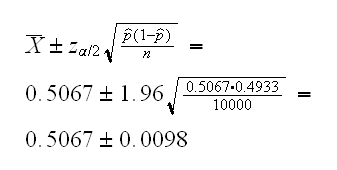
so (0.4969, 0.5165) is a 95% confidence interval for p.
Example the South African mathematician Jon Kerrich, while in a German POW camp during WWII, tossed a coin 10000 times. He got 5067 heads (and of course 4933 tails) We want to find an interval estimate for p=P("heads")
A frequentist approach to this problem would be as follows: the maximum likelihood estimator of p is 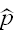 =X̄, the sample mean. By the Central Limit Theorem X̄~N(p,√(pq/n)), so a 100(1-α)% confidence interval for p is given by
=X̄, the sample mean. By the Central Limit Theorem X̄~N(p,√(pq/n)), so a 100(1-α)% confidence interval for p is given by
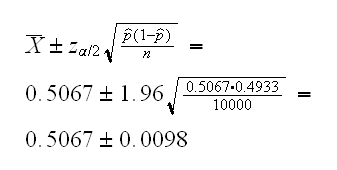
so (0.4969, 0.5165) is a 95% confidence interval for p.
How about a Bayesian analysis? In that case we first need a prior distribution on p, the true probability of heads.
Let's first try the "standard" prior for this model, p~Beta(α,β). Then

and so we see that the posterior distribution is the beta-binomial.
How can we get an interval estimate from the posterior? There are several methods, one of them uses equal tail probabilitites: find L and H such that
P(p<L|y)=P(p>H|y)=α/2
So L=qbeta(α/2,y+α,n-y+β) and H=qbeta(1-α/2,y+α,n-y+β)
What should we choose as the parameters for the prior distribution? First off it probably makes sense here to choose α=β because then E[p]=α/(α+β)=1/2 and of course we do expect a coin to be fair. Say α=β=m.
Moreover, V[p]=m2/(2m)2/(2m+1)=1/(8m+4), so the larger m the more concentrated our prior is around 1/2. Also, note that p|y=5067~Beta(5067+m,4933+m), so whether m=1 or m=100 really makes very little difference here. Say we pick m=10, then
(L,H)= (0.4969,0.5165)
which is exactly the same as the frequentist confidence interval.
As an alternative method for finding an interval we could also do a simulation, generate data from the posterior distribution and find the 2.5th and 97.5th percentile of the data. This is done in
bayes.fun(1)
The prior above is probably not a very good choice. In real life we would probably have a strong believe that any coin is fair or close to it. On the other hand if it turns out a coin is not fair, then we probably have very little knowledge what p might be (before ever flipping it), so a more reasonable prior might be one that puts more probability to p close to 1/2, and then the rest of the probability uniformly on [0,1]. Here is one such prior, where a depends on our belief that p=1/2. The curve is drawn in
bayes.fun(2)
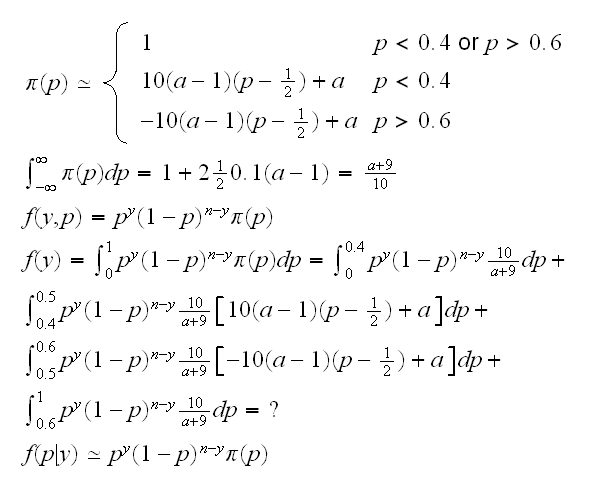
This time finding the marginal is a bit tricky (put possible!) Even if we could do it, we would still have the problem to solve the equation P(p<L|p)=α/2, which would surely have to be done numerically.
How about the second idea, to simulate data from the posterior distribution? Again at first this seems to be impossible, because we only know the posterior distribution up to a constant (the marginal), so for example the accept-reject algorithm won't work. Remarkably, using a technic called Markov Chain Monte Carlo this simulation can still be done, see
bayes.fun(3)