Expectations
The expectation (or expected value) of a random variable g(X) is defined by
We use the notation Eg(X)
**Example** : we roll fair die until the first time we get a six. What is the expected number of rolls?
We saw that f(x) = 1/6*(5/6)^x-1 if x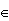{1,2,..}. Here we just have g(x)=x, so
How do we compute this sum? Here is a "standard" trick:
and so we find
X is said to have a uniform [A,B] distribution if f(x)=1/(B-A) for AExpectations of Random Vectors
The definition of expectation easily generalizes to random vectors:
**Example** Let (X,Y) be a discrete random vector with f(x,y) = (1/2)^x+y, x$\ge$1, y$\ge$1. Find E[XY^2]
Covariance and Correlation
The covariance of two r.v. X and Y is defined by cov(X,Y)=E[(X-μ_X)(Y-μ_Y)]
The correlation of X and Y is defined by cor(X,Y)=cov(X,Y)/(σ_Xσ_Y)
Note cov(X,X) = V(X)
As with the variance we have a simpler formula for actual calculations: cov(X,Y) = E(XY) - (EX)(EY)
**Example** : take the Example of the sum and absolute value of the difference of two rolls of a die. What is the covariance of X and Y?
So we have
μ_X = EX = 2*1/36 + 3*2/36 + ... + 12*1/36 = 7.0
μ_Y = EY = 0*6/36 + 1*12/36 + ... + 5*2/36 = 70/36
EXY = 0*2*1/36 + 1*2*0/36 + .2*2*0/36.. + 5*12*0/36 = 490/36
and so cov(X,Y) = EXY-EXEY = 490/36 - 7.0*70/36 = 0
Note that we previously saw that X and Y are **not** independent, so we here have an example that a covariance of 0 does **not** imply independence! It does work the other way around, though:
**Theorem**: If X and Y are independent, then cov(X,Y) = 0 ( = cor(X,Y))
proof (in the case of X and Y continuous):
and so cov(X,Y) = EXY-EXEY = EXEY - EXEY = 0
**Example** Consider again the example from before: we have continuous rv's X and Y with joint density f(x,y)=8xy, 0$\le$xConditional Expectation and Variance
Say X|Y=y is a conditional r.v. with density (pdf) f. Then the conditional expectation of X|Y=y is defined by
Let E[X|Y] denote the function of the random variable Y whose value at Y=y is given by E[X|Y=y]. Note then Z=E[X|Y] is itself a random variable.
**Example**: An urn contains 2 white and 3 black balls. We pick two balls from the urn. Let X be denote the number of white balls chosen. An additional ball is drawn from the remaining three. Let Y equal 1 if the ball is white and 0 otherwise.
For example f(0,0) = P(X=0,Y=0) = 3/5*2/4*1/3 = 1/10.
The complete density is given by:
| **x** |
**0** |
**1** |
**2** |
| **P(X=x)** |
3/10 |
3/5 |
1/10 |
and
| **x** |
**0** |
**1** |
**2** |
| **P(X=x|Y=0)** |
1/6 |
2/3 |
1/6 |
and so E[X|Y=0] = 0*1/6+1*2/3+2*1/6 = 1.0
The conditional distribution of X|Y=1 is
| **z** |
**1** |
**1/2** |
| P(Z=z) |
3/5 |
2/5 |
with this we can find E[Z] = E[E[X|Y]] = 1*3/5+1/2*2/5 = 4/5
How about using simulation to do these calculations? - program **urn1**
**Example** Consider again the example from before: we have continuous rv's X and Y with joint density f(x,y)=8xy, 0$\le$x
Find the marginal distribution of X
![](graphs/prob415.png" >
Find the marginal distribution of Y
![](graphs/prob414.png" >
Find the conditional pdf of Y|X=x
Note: this is a proper pdf for any fixed value of x
Find E[Y|X=x]
![](graphs/prob417.png" >
Let Z=E[Y|X]. Find E[Z]
![](graphs/prob418.png" >