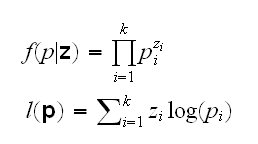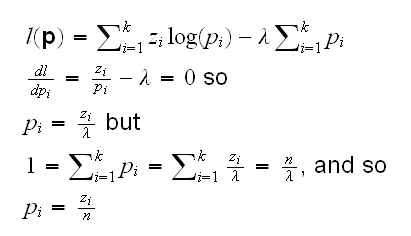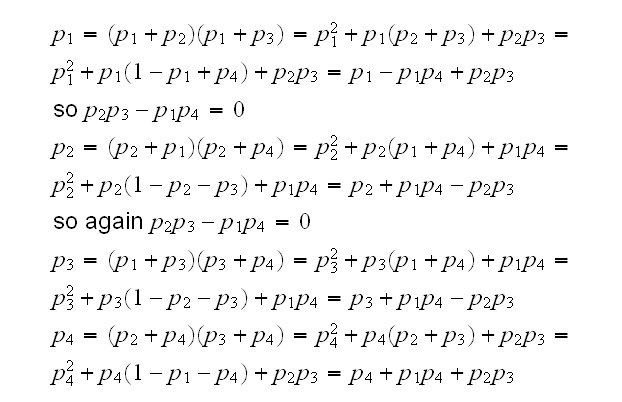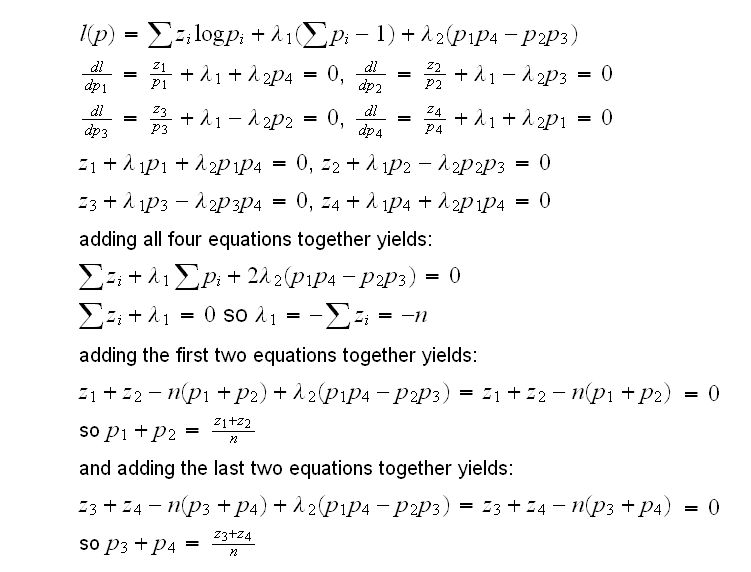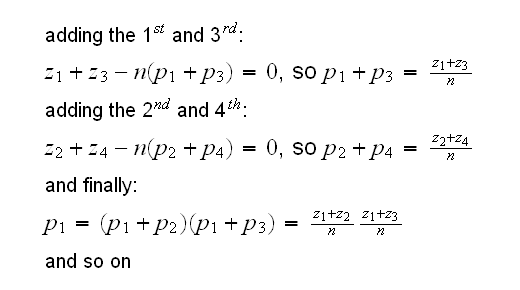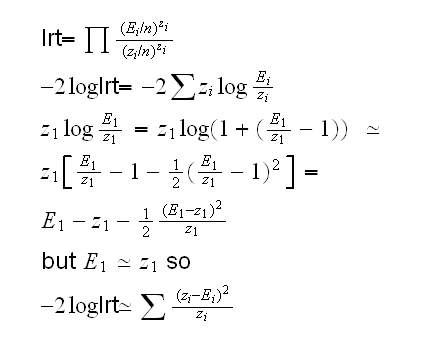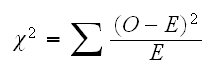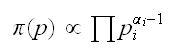Example Psychological and social factors can influence the survival of patients with serious diseases. One study examined the relationship between survival of patients with coronary heart disease and pet ownership. Each of 92 patients was classified as having a pet or not, and whether they survived one year. Here is the data, from Erika Friedmann et al., "Animal companions and one-year survival of patients after discharge from a coronary care unit.":
| Patient Status |
Owns a Pet |
Does not Own a Pet |
| Alive |
50 |
28 |
| Dead |
3 |
11 |
Question: is there a statistically significant relationship (association) between Ownership and Survival?
What is an appropriate probability model here? For each patient in the population there are four possibilities: owns a pet-alive, owns a pet-dead, does not own a pet-alive, does not own a pet-dead. We can model this using a multinomial distribution: (X,Y) takes values (1,1), (1,2), (2,1), (2,2) with P((X,Y)=(i,j))=pij. Of course we have
0≤pij≤1 and ∑∑pij=1
The math that follows get's a little easier if we reparametrize the problem as follows: discrete random vector with finitely many values is always equivalent to a mulitnomial distribution. So let Z be a rv with values 1-4 and probabilities p1,..,p4
Let's begin by finding the mle's of the pi's. Let zi=∑I[Z=i], then
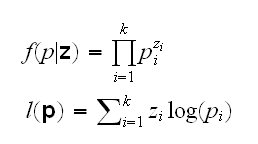
Now we need to be careful because we need to maximize this function with the additional condition ∑pi=1 (otherwise the maxima is at infinity anyway), so we need to use Lagrange multipliers:
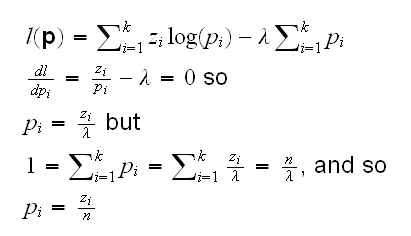
What does our question mean in terms of the pi's? If there is no relationship between Ownership and Survival then X and Y are independent and we find P((X,Y)=(i,j))=P(X=i)P(Y=j) for i,j=1,2, or
p1=(p1+p2)(p1+p3)
p2=(p1+p2)(p2+p4)
p3=(p1+p3)(p3+p4)
p4=(p2+p4)(p3+p4)
It's easy to see why if you think in terms of marginals:
| Patient Status |
Owns a Pet |
Does not Own a Pet |
|
| Alive |
p1 |
p2 |
p1+p2 |
| Dead |
p3 |
p4 |
p3+p4 |
| |
p1+p3 |
p2+p4 |
|
So let's do the LRT test for this problem:
H0: X indep. of Y equiv. H0: above equations hold
we already found the mle's, so now we need to find the numerator. First note that:
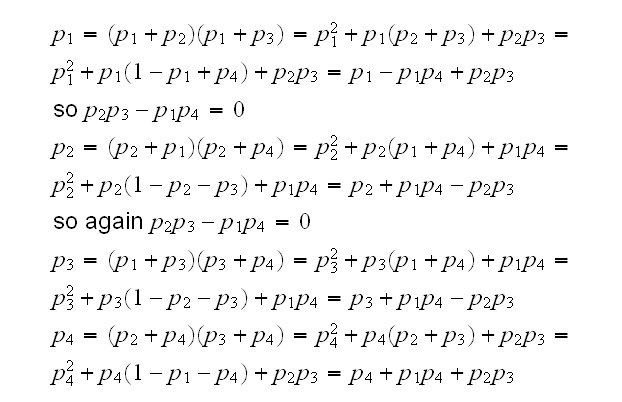
so we need to maximize l(p)=∑zilog(pi) under the constraints ∑pi=1 and p1p4-p2p3=0. Again we use Lagrange multipliers:
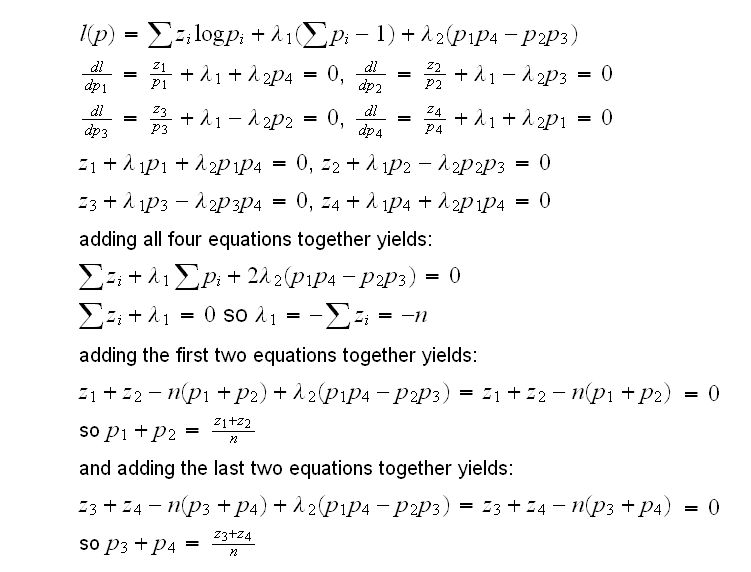
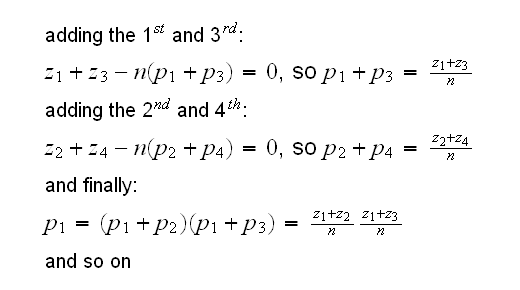
Now let E1=(z1+z2)(z1+z3)/n, and so on, then
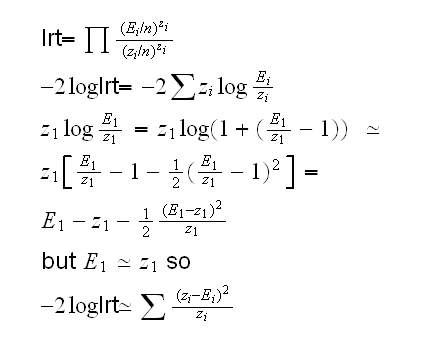
which shows how one eventually ends up with the famous chisquare statistic:
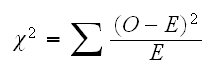
for our data we have E1=(z1+z2)(z1+z3)/n = (50+28)(50+3)/92=44.9 and so on:
| Patient Status |
Owns a Pet |
Does not Own a Pet |
| Alive |
0=50, E=44.9 |
O=28, E=33.1 |
| Dead |
O=3, E=5.9 |
O=11, E=8.1 |
so χ2=(50-44.9)2/44.9+(28-33.1)2/33.1+(3-5.9)2/5.9+(11-8.1)2/8.1=8.85
this has a chisquare distribution with 1(=(r-1)(c-1)) df, so the p-value is 1-pchisq(8.85,1)=0.003
So again we see that one of the famous methods in Statistics derives from the likelihood ratio test (plus some extra approximations)
Bayesian Analysis
as always this starts with a prior. If we again use the parametrization (p1,..,p4) then Z=(z1,..,z4) has a multinomial distribution (n,p1,..,p4) where n is assumed to be known. A conjugate prior for the multinomial is the Dirichlet distribution with pmf
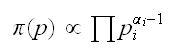
and then π(p|z) ~ D(n,α1+z1,..,α4+z4) The choice of α1=..=α4=1is a non-informative prior (pi=1/k). The null hypothesis of independence then means independence of the posterior distribution, same as above. Indeed, under the non-informative prior we could again recover the chisquare test.