Distributions Arising in Statistics

In this chapter we briefly discuss some distributions that often come up in Statistics.

Chisquare Distribution

Definition

a random variable X is said to have a chisquare distribution with n degrees of freedom, X~χ2(n), if it has density

Of course we have X~Γ(n/2,2)

Say Z~N(0,1) and let X=Z2. then if x>0

so X~χ2(1)

We have the following properties of a χ2:

Theorem

Say X~χ2(n), Y~χ2(m) and X and Y are independent. Then

From this theorem it follows that if Z1,..,Zn are iid N(0,1), then ∑Zi2~χ2(n)

Definition

Say X1, .., Xn are a sample, then the sample variance is defined by

Theorem

Say X1, .., Xn are iid N(μ,σ), then (n-1)S2/σ2~χ2(n-1)

Note: we use "n-1" instead of "n" because then S2 is an unbiased estimator of σ2, that is E[S2]=σ2

Note: another important feature here is thatX̅ 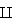S2

Student's t Distribution (by W.S. Gosset)

Definition

Say X~N(0,1), Y~χ2(n) and X 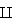Y. Then

has a Student's t distribution with n degrees of freedom, Tn~t(n), that is

Note Tn → N(0,1) in distribution

We have ETn=0 if n>1 (and does not exist if n=1) and VTn=n/(n-2) if n>2 (and does not exist if n≤2)

The importance of this distribution in Statistics comes from the following:

Theorem

say X1, .., Xn are iid N(μ,σ). Then

Note: S is of course an estimate of the population standard deviation, so this formula tries to standardize the sample mean without knowing the exact standard deviation.

An important special case is X~t(1). This is also called the Cauchy distribution. Notice it has no finite mean (and of course then also no finite variance). It has density

Snedecor's F distribution

Definition

X is said to have an f distribution with n and m degrees of freedm, X~F(n,m) if

Theorem

Say X~χ2(n), Y~χ2(m) and X and Y are independent. Then (X/n)/(Y/m)~F(n,m)


We have EF = m/(m-2) (no mention of n !)

Theorem

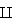Say X1, .., Xn are iid N(μx,σx) and Y1, .., Ym are iid N(μy,σy). Furthermore XiYj for all i and j. Then

Order Statistics

Many statistical methods, for example the median and the range, are based on an ordered data set. In this section we study some of the common distributions of order statistics.

One of the difficulties when dealing with order statistics are ties, that is the same observation appearing more than once. This should only occur for discrete data because for continuous data the probabiltity of a tie is zero. They may happen anyway because of rounding, but we will ignore them in what follows.

Say X1, .., Xn are iid with density f. Then X(i) is the ith order statistics if X(1)< ... < X(i) < ... <X(n)

Note X(1) = min {Xi} and X(n) = max {Xi}

Let's find the pdf of X(i). For this let Y be a r.v. that counts the number of Xj ≤ x for some fixed number x. We can think of Y as the number of "successes" of n independent Bernoulli trials with success probability p = P(Xi ≤ x) = F(x) for i=1,..,n. So Y~B(n,F(x)). Note also that the event {Y≥i} means that more than i observations are less or equal to x, so the ith largest is less or equal to x. Therefore

taking derivatives one can show that


Example : Say X1, .., Xn are iid U[0,1]. Then for 0<x<1 we have f(x)=1 and F(x)=x. Therefore

Empirical Distibution Function

The empirical distribution function of a sample X1, .., Xn is defined as follows:

so it is the sample equivalent of the regular distribution function:

• F(x)=P(X≤x) is the probability that the rv X≤x

• F̂(x) is the proportion of X1, .., Xn ≤x

The empirical distribution function is very important in Statistics.

Example: say we have data

0.36 0.37 0.37 0.46 0.47 0.52 0.54 0.67 0.96 0.98

then the edf is

Here is the edf of a random sample of 100 from a N(0,1), together with the true cdf: