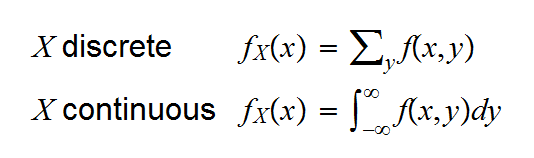
Definition
Say we have a random vector with joint pmf (pdf) f(x,y).
a) the marginal pmf (pdf) of X is given by
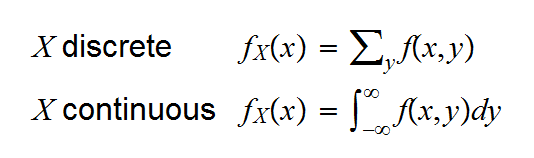
b) the conditional random variable X|Y=y has pmf (pdf)
fX|Y=y(x|y) = f(x,y)/fY(y)
Example: say we have a discrete random vector (X,Y) with pmf
| X/Y | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0.1 | 0.1 | 0.2 |
| 1 | 0 | 0.3 | 0.3 |
a) find fX and fY`
| X/Y | 0 | 1 | 2 | fX |
|---|---|---|---|---|
| 0 | 0.1 | 0.1 | 0.2 | 0.4 |
| 1 | 0 | 0.3 | 0.3 | 0.6 |
| fY | 0.1 | 0.4 | 0.5 | 1 |
| x | 0 | 1 |
|---|---|---|
| fX(x) | 0.4 | 0.6 |
| y | 0 | 1 | 2 |
|---|---|---|---|
| fY(y) | 0.1 | 0.4 | 0.5 |
b) find EX, VarX, EY, VarY
EX = 0*0.4+1*0.6 = 0.6
EX2 = 02*0.4+12*0.6 = 0.6
VarX = EX2-(EX)2 = 0.6-0.62 = 0.24
σx=√VarX = √0.24 = 0.489
EY = 0*0.1+1*0.4+2*0.5 = 1.4
EY2 = 02*0.1+12*0.4+22*0.5 = 2.4
VarY = EY2-(EY)2 = 2.4-1.42 = 0.44
σy=√VarY = √0.44 = 0.663
Definition Say we have two random variables X and Y, then
a) covariance Cov(X,Y) = E[(X-μx)(Y-μy)] = EXY=EXEY
b) correlation Cor(X,Y) = Cov(X,Y)/(σxσy)
Definition two random variables X and Y are independent if and only if
f(x,y)=fX(x)fY(y) for all x and y
Note: if X and Y are independent then cov(X,Y)=0
the reverse is not true in general, but is true if X and Y have a normal distribution
Example say we have a discrete random vector (X,Y) with pmf
| X/Y | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0.1 | 0.1 | 0.2 |
| 1 | 0 | 0.3 | 0.3 |
a) Find Cor(X,Y)
Cor(X,Y) = Cov(X,Y)/(σxσy)
Cov(X,Y) = EXY-EX*EY
EXY=0*0*0.1+0*1*0.1+...+1*2*0.3 = 0.3+2*0.3 = 0.9
Cov(X,Y) = EXY-EX*EY = 0.9-0.6*1.4 = 0.06
Cor(X,Y) = Cov(X,Y)/(σxσy) = 0.06/(0.489*0.663) = 0.185
b) Are X and Y independent?
No, because Cov(X,Y)≠0
or
f(0,0) = 0.1 ≠ fX(0)fY(0)= 0.1*0.4=0.04
Example say we have a discrete random vector (X,Y) with pmf
| X/Y | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0.1 | 0.1 | 0.2 |
| 1 | 0 | 0.3 | 0.3 |
find fX|Y=y
Y=0:
fX|Y=0(x|0) = f(x,0)/fY(0)
fX|Y=0(0|0) = f(0,0)/fY(0) = 0.1/0.1 = 1
fX|Y=0(1|0) = f(1,0)/fY(0) = 0/0.1 = 1
fX|Y=0(0|0)=1
Y=1
fX|Y=1(x|1) = f(x,1)/fY(1)
fX|Y=1(0|1) = f(0,1)/fY(1) = 0.1/0.4 = 0.25
fX|Y=1(1|1) = f(1,1)/fY(1) = 0.3/0.4 = 0.75
| x | 0 | 1 |
|---|---|---|
| fX|Y=1(x|1) | 0.25 | 0.75 |
Y=2
fX|Y=2(x|2) = f(x,2)/fY(2)
fX|Y=2(0|2) = f(0,2)/fY(2) = 0.2/0.5 = 0.4
fX|Y=2(1|2) = f(1,2)/fY(2) = 0.3/0.5 = 0.6
| x | 0 | 1 |
|---|---|---|
| fX|Y=2(x|2) | 0.4 | 0.6 |
Definition
the conditional expected value of X|Y=y is just the expected value of the conditional random variable X|Y=y
Example say we have a discrete random vector (X,Y) with pmf
| X/Y | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0.1 | 0.1 | 0.2 |
| 1 | 0 | 0.3 | 0.3 |
Find E[X|Y=y]
Y=0: E[X|Y=0] = 0*1 = 0
Y=1: E[X|Y=1] = 0*0.25+1*0.75 = 0.75
Y=2: E[X|Y=2] = 0*0.4+1*0.6 = 0.6
Example: say the random vector (X,Y) has joint pdf f(x,y)=cx, 0<x<y2<1. Find E[X|Y=y]
The area where f>0 is shown here:
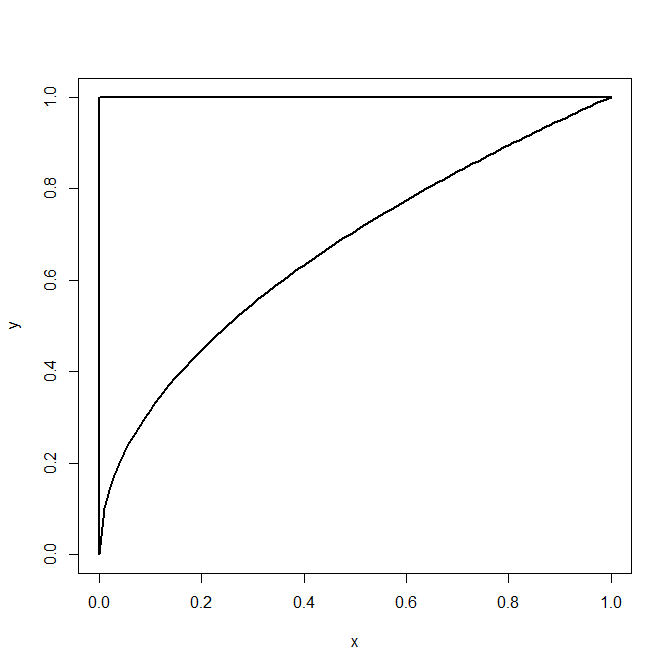
so
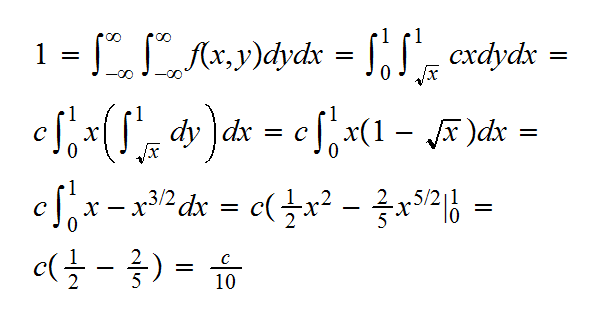
and so c=10
Now
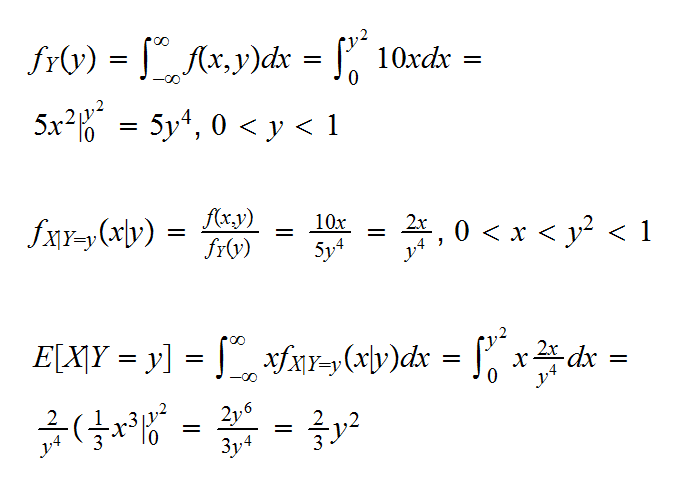
Example say we have random variables X,Y~U[0,1] and independent. Find the density of Z=X+Y