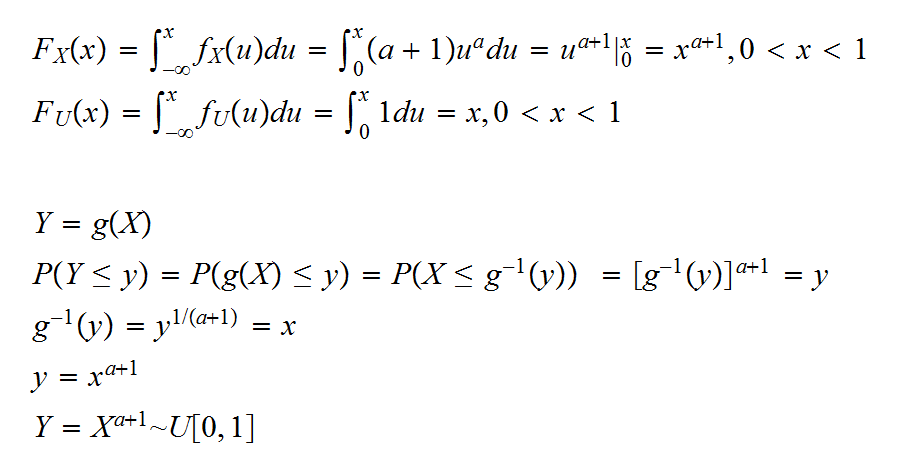
We are not going to do a detailed review of the theory of probability. Instead we are going to do through several examples that include the kinds of calculations you should know how to do.
Definition
A random variable X is a function from a sample space to the real numbers.
Example: Say we roll a fair die twice. Let X be the sum of the dice.
Here the sample space is
S={(1,1), (1,2), .., (6,6)}
and for example X(3,4) = 7
Now P(X=4) = P( {(1,3), (2,2), (3,1) } = 3/36 = 1/12
The cumulative distribution function of a random variable X is given by
F(x) = P(X≤x)
Example: Say we roll a fair die twice. Let X be the sum of the dice. Then
F(x)=0 if x<2
F(x) = P(X=2) = 1/36 if 2 ≤x<2
F(x) = P(X=2 or X=3) = 3/36 if 3 ≤x<4

Definition
Random variables come in two forms: if X has countably many values it is called discrete, otherwise continuous. A discrete rv is described by its probability mass function pmf given by f(x)=P(X=x), a continuous rv X by its density f(x)=F'(x)
Definition
the expected value of a random variable X is defined by
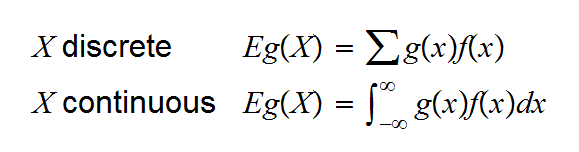
The most import expected values are
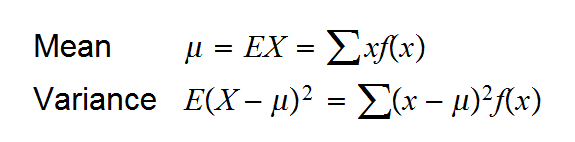
we write VarX for the variance. Often we also consider the standard deviation σ=√VarX
and we have the formula
Var(X)=EX2-(EX)2
Example: say X is a discrete uniform rv on {1,..,N}
a) Find its pmf
"uniform" means that P(X=i)=P(X=j) for all 1≤i,j≤N. So
∑P(X=i) = ∑P(X=1) = N*P(X=1) = 1 or P(X=1)=1/N or
f(x) = 1/N for 1≤i≤N
b) Find EX and VarX
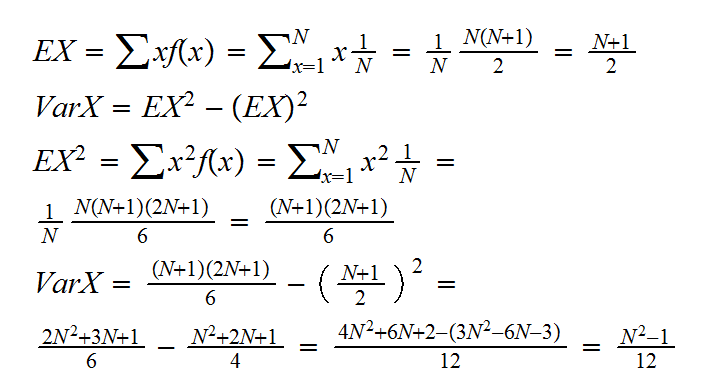
Example say we have a random variable X with density f(x)=cxa, 0<x<1, a>1
a) find c
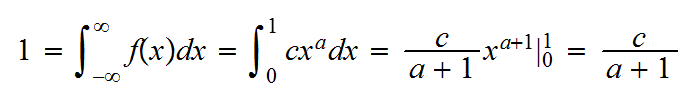
and so c=a+1
b) Find EX and VarX
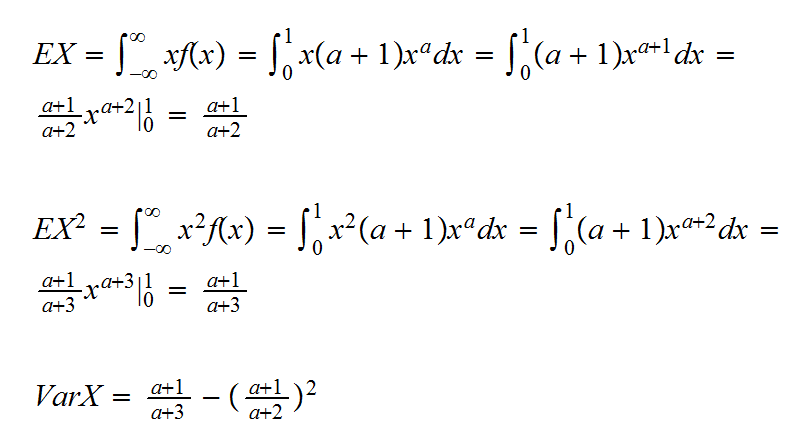
c) Does there exist a function g such that the rv Y=g(X) has a U[0,1] distribution?