Example Say we have X1, .., Xn ~ Pois(λ) and we want to test H0: λ=λ0 vs. H1: λ > λ0
We know that X̅ is the mle of λ, so a test based on X̅
seems reasonable.
Clearly large values of X̅ will indicate that the alternative is more likely to be true than the null hypothesis, so a reasonable rejection region is {X̅>cv}. To find cv we need to solve the equation
α = P(X̅>cv | λ=λ0) = 1 - P( X1+..+Xn ≤ n·cv | λ=λ0),
but under the null hypothesis
Xi~P(λ0)
so
Sn = X1+..+Xn ~ P(nλ0)
so cv = qpois(1-α,nλ0)/n
The p-value of the test is
p=P(Y> s n | λ=λ0)
where Y~P(nλ0)
What if we want to test
H0: λ=λ0 vs. H1: λ≠λ0
Now the critical region could be
{X̅<cv1 or X̅>cv2}
Again the choice of cv1 and cv2 is not unique. For example , cv1 = 0 and cv2 = qpois(1-α,nλ0)/n would work. As before we can devide α in two:
cv1 = qpois(α/2,nλ0)/n and cv2 = qpois(1-α/2,nλ0)/n.
The p-value now is found by
So the idea here is this:
• Find a point estimator for the parameter in question, say S
• Find a function of S, say T(S), such that you know the distribution of T(S) and can solve the equation
α = P(T(S)<c)
A special case of this idea used the following
Definition
A function T of the data and the parameters is called a pivot if the distribution of T does not depend on the parameters
Example: Say X1, .., Xn ~ N(μ,σ), then
T = √n(X̅ -μ)/σ ~ N(0,1)
and therefore is a pivot.
Example: say we the following sample from a N(μ,10) and we want to test at the 5% level
H0: μ=50 vs Ha: μ>50
66.5 55.3 78 63.1 65.5 51.2 56.6 64.9 71.8 58.4 58.7 70.4 53.7 66 48.1 60.6 62.9 70.6 44.8 54.4
54.4 37.2 77.1 48.7 55.8
Now we should reject H0 if X̅>c, which is equivalent to T>c, and so
0.05 = α =P(T>c')
so c'=1.65
Now X̅ = 59.788, so T=√25(59.788-50)/10 = 4.894 > 1.65,
so we reject the null hypothesis.
A test based on Zn = (Tn-θ)/Sn is often called a Wald test.
Example : Let X1, .., Xn be iid Ber(p). Consider testing
H0: p=p0 vs. Ha: p≠p0
The MLE of p is p̂ =X̅, so the CLT applies and states that for any p
Of course we don't know p, but again we can estimate the p's in the denominator by p̂ and so we get a test with the test statistic
and we reject the null hypothesis is |Zn| > za/2.
Instead of replacing the p's in the denominator by p̂ we could also have used p0. Then another test is based on
which rejects the null hypothesis if |Z'n| > za/2.
Which of these tests is better? Well, that depends on the power function. Here are the curves for p0=0.2, the one for Zn in blue:
As we see the power curves cross, so it depends on the true value of p which test is better. If we suspect that p>0.2 we might prefer the Z' test, otherwise the Z test.
Definition
Say we want to test H0: θ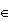 
θ0 vs. H1: θ 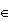θ0c. Then the likelihood ratio test statistic is defined by
A likelihood ratio test (LRT) is any test that has a rejection region of the form {x: λ(x) ≤ c}
The constant c here is not important, it will be found once we decide on the type I error probability α. It may better to think of this as
"reject H0 if λ(x) is small"
Note that the supremum in the denominator is found over the whole parameter space, so this is just like finding the mle, and then finding the corresponding value of the likelihood function.
Note that in the numerator we find the supremum over a subset of the one used in the denominator, so we always have
λ(x) ≤ 1
The logic of the LRT is this: In the denominator we have the likelihood of observing the data we did observe, given the most favourable paramaters (the mle) possible. In the numerator we find the likelihood assuming the null hypothesis is true. If their ratio is much smaller than 1, then there are parameters outside the null hypothesis which are much more likely than any in the null hypothesis, and we would reject the null hypothesis.
Example : Let X1, .., Xn be a sample from N(θ,1). Consider testing H0: θ=θ0 vs. H1: θ≠θ0. Here Θ0={θ0} and so the numerator of λ(x) is L(θ0|x). For the denominator we have to find sup{L(θ|x),θ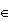 
}:
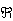and so
Now an LRT test rejects the null hypothesis if λ(X) < c for some constant c. c depends on the choice of α. Again it is best to think of the test as rejecting H0 if "λ(X) is small". But
λ(X)=exp{-n/2(X̅-θ0)2} is small iff
-n/2(X̅-θ0)2 is small iff
(X̅-θ0)2 is large iff
|X̅-θ0| is large, say |X̅-θ0|>c
In other words the LRT test rejects the null hypothesis if λ(X) is small, which is equivalent to |X̅-θ0| being large.
What is the constant c? It depends on α, namely
so c = zα/2/√n
For example , say n=10 and we want α=0.05, then c = z0.025/√10 = 1.96/√10 = 0.62
Example : You are at a charity event. There is going to be a raffle, with the grand price a car! A ticket costs $100, so you decide to by one if your chance of winning is at least 1 in 100. The tickets are numbered from 1 to N. You walk around a little and you see the following tickets:
21 45 68 91
Should you buy a ticket?
If a total of N tickets are sold, your chance of winning is 1/N, so you should buy one of N≤100. Therefore we need to do a hypothesis test
H0: N0≤100 vs Ha: N0>100
What is our probability model? Let Xi be the number on the ith ticket. The exact distribution of X1, .., Xn is bit complicated because each ticket is unique, so Xi ≠ Xj. We will simplify this a bit by ignoring this issue. Then we can assume that the Xi are independent and
X1, .., Xn ~U{1,..,N}, or
Note that I{M,..}(M} =1 always but I{M,..}(N0) could be 0 or 1 because we don't know what N0 is.
Here is what this looks like as a function of M:
so here
"λ(x) is small" is the same as "M is small or M is large"
Because we are interested in the alternative N0>100 we can ignore the "M is small" option, and we get the rejection region
reject H0 if M>c
This of course makes perfectly good sense: if we see a ticket with a large number, this tells us that many tickets have been sold and we should not buy one!
So, how about c? As always it depends on α:
Using α=0.05 we find
c = N0(1-α)1/n = 100(1-0.05)1/5 = 98.97 = 99
so as long as the ticket with the largest number is 98 or less, we should buy one.
Definition
Suppose X1, .., Xn are iid f(x|θ) and we wish to test
H0: θ 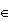Θ0 vs. H1: θ 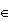Θ0c
Then under some regularity conditions the distribution of -2logλ(X) converges to the distribution of a χ2(p). Here p is difference of the number of free parameters in Θ and the number of free parameters in Θ0.
Example We flip a coin 1000 times and find 545 heads. Test at the 5% whether this is a fair coin.
we have
X1, .., Xn~Ber(p)
and we want to test
H0:p=p0 vs Ha:p≠p0
Let's find the LRT test for this problem. First we have
Here is what that looks like for n=1000 and p0=0.5:
and it is clear that
λ(x) is small iff k small or large relative to np0 iff |k-np0| large
Now let Y = ∑Xi~Bin(n,p0), so
α = P(|Y-np0|>cv) =
1-P(|Y-np0|≤cv) =
1- P(-cv ≤ Y-np0 ≤ cv) =
1- P(np0-cv ≤ Y ≤ np0+cv)
For our test we have n=1000, p0=0.5 so np0 = 500. Now
| cv | Prob |
|---|---|
| 20 | 0.097 |
| 21 | 0.087 |
| 22 | 0.077 |
| 23 | 0.069 |
| 24 | 0.061 |
| 25 | 0.053 |
| 26 | 0.047 |
| 27 | 0.041 |
| 28 | 0.036 |
| 29 | 0.031 |
| 30 | 0.027 |
and using α=0.05 we find cv=26, and so we reject the null hypothesis because
|k-np0| = |545-1000·0.5| = 45 > 26
We conclude that the coin is not fair.
How about using the chisquare approximation? In that case
T = -2logλ(x)~χ2(1), so
and again we reject H0, now because
T=8.11 > cv=3.8
Notice if the null hypothesis specifies on parameter, we have
T = -2logλ(x) ~ χ2(1)
and we reject H0 if T>c. But if Z~N(0,1), then Z2~χ2(1), so
α = P(T>c) = P(Z2>c) = 1-P(Z2<c) = 1-P(-√c<Z<√c) = 1-(2Φ(√c)-1)
Φ(√c) = 1-α/2
√c = zα/2
c = zα/22
Why do we have this approximation? In essence it is the following idea:
so the likelihood ratio is a sum of iid rv's, and so the central limit theorem applies.
Example : (two- sample problem)
in a company two employees perform the same task. The company wants to find out whether it takes them the same time to do the task. So they time them and find (in minutes):
Employee 1: 7.3 8.5 8.7 9.0 9.2 9.3 9.4 9.5 9.6 9.6 9.7 9.8 9.9 9.9 10.0 10.1 10.3 10.5 10.8 11.2
Employee 2: 8.7 9.6 9.7 10.1 10.1 10.4 10.6 10.8 10.8 10.9 10.9 11.2 11.3 11.4 11.4 12.0 12.2
Say the true mean time for employee 1 is μ and for employee 2 it is τ. Then we want to test
H0: μ=τ vs. Ha:μ≠τ
Here is a first look at the data:
From this it seems reasonable to model the times as coming from a normal distribution. So we have
X1, .., Xn~N(μ,σx), Y1, .., Ym~N(τ,σy)
Moreover
sd(x)=086
sd(y)=0.89
and so we will assume that σx=σy=σ
Finally to keep things easy we will assume that σ=0.875 is known. Then we find
X̅ = 9.615
Y̅ = 10.712
X̅Y̅ = 10.119
∑(x-X̅)2 = 13.9
∑(y-Y̅)2 = 12.658
∑(x-X̅Y̅ )2 = 18.984
∑(y-X̅Y̅ )2 = 18.633
-2logλ(x,y) = 1/0.8752*( 18.984 + 18.633 - 13.9 - 12.658) = 14.4
Here we have p = 2-1, so if we test at the 5% level we again find c=3.8, but
T = 14.4 > 3.8
so we reject the null hypothesis.
A little more:
Of course this is a bit wild: first, is it true that
• the difference of two independent chisquare rv's is chisquare? Actually, yes
• but is Sxy independent of Sx and Sy? Actually, no, but it works here because of the normal distribution.
Notice that in this problem ultimately the likelihood ratio statistic is a function of the sample variances. This is still true if we had three or more groups, and then this type of problem is appropriately called Analysis of Variance.