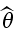 = T(X1, ..,Xn) is called unbiased for θ if
= T(X1, ..,Xn) is called unbiased for θ if Definition
An estimator 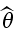 = T(X1, ..,Xn) is called unbiased for θ if
= T(X1, ..,Xn) is called unbiased for θ if
E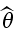 =θ
=θ
B(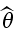 ) = E
) = E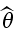 -θ
-θ
is called the bias of the estimator T
Example: say X1, ..,Xn are iid with mean μ and standard deviation σ. Then
EX̅ = E[(1/n)∑Xi] = (1/n)∑E[Xi] = (1/n)∑μ = (1/n)*nμ = μ
so X̅ is an uniased estimator of μ
How about the variance σ2? Here we will use as an estimator the sample variance
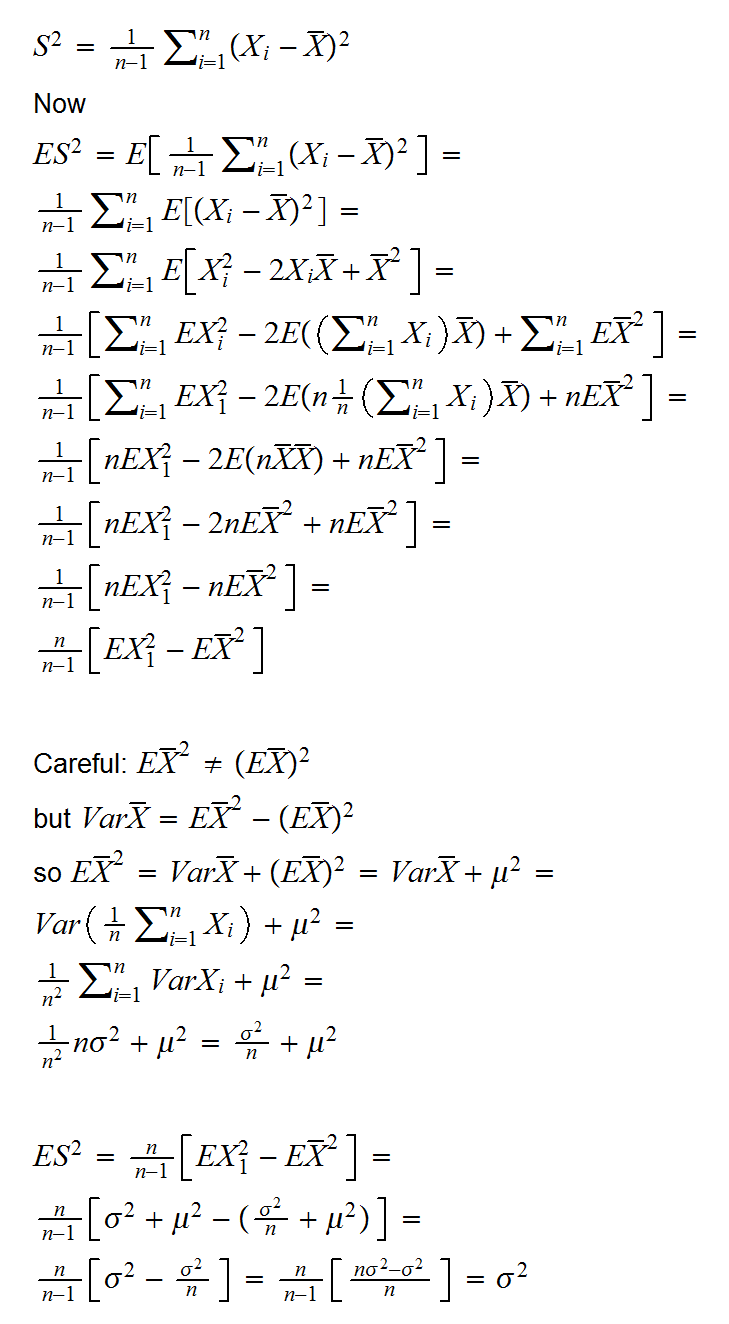
and this of course explains why we use "n-1" instead of "n".
How about the standard deviation σ? Unfortunately
E√S2 ≠ √ES2
(actually, a famous inequality called Jensen's inequality says E√S2 ≤ √ES2)
so S = √S2 is NOT an unbiased estimator of the standard devation s. In fact, in this generality nothing more can be said. Howerver, if we also assume that the Xi come from a normal distribution it can be shown (Holzman 1950) that
E[cnS]=σ
where
cn = {Γ[(n-1)/2][(n-1)/2)]1/2}/Γ(n/2)
Surprised that the Gamma function shows up here? Remember that if Xi,..,Xn is iid Normal, S2 has a chisquared distribution and the chisquare is a special case of thr Gamma distribution.
Example: say X1, ..,Xn are iid U[0,θ]. Find an unbiased estimator of θ.
we have Xi<θ for all i, so max{Xi}<θ as well. In fact we would expect the largest of the Xi to be close to θ. So let's try as an extimator T=max{Xi}
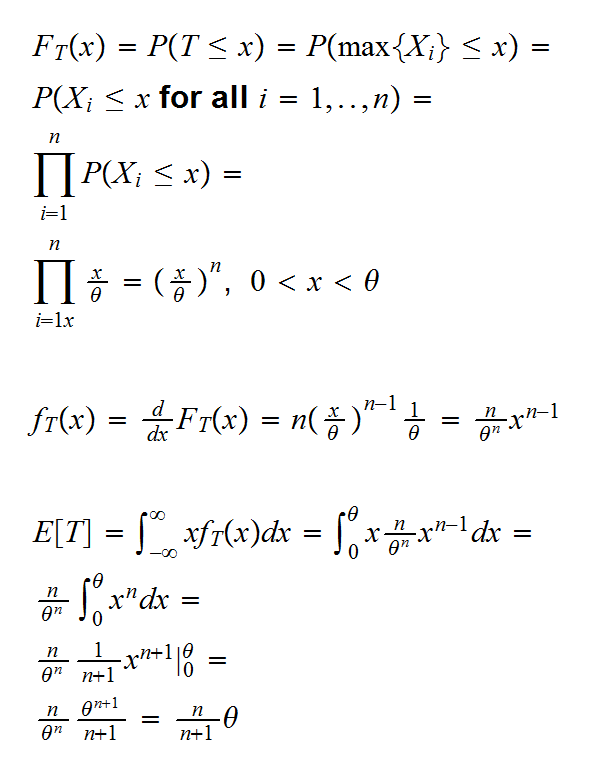
so T is not an unbiased estimator of θ, but of course it is easy to make it so, just use (n+1)/nθ!
Let X = X1, ..,Xn be a sample from a distribution with pmf(pdf) f(x|θ1,..,θk).
Definition
the ith sample moment is defined by
mi = (Xi1+..+Xin)/n
Analogously define the ith population moment by
μi = EXi
Of course μi is a function of the θ1,..,θk. So we can find estimators of θ1,..,θk by solving the system of k equations in k unknowns
mi=μi i=1,..,k
Example: say X1, ..,Xn are iid U[0,θ]
we have
so we get
m1 = μ1 = θ/2
or 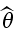 = 2m1 = 2X̅
= 2m1 = 2X̅
Example : say X1, ..,Xn are iid N(μ,σ).
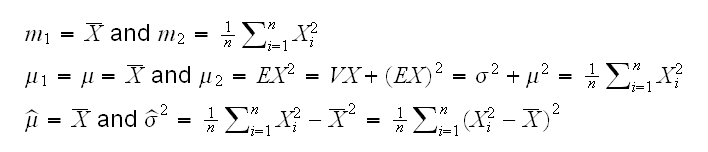
The idea here is this: the likelihood function gives the likelihood (not the probability!) of a value of the parameter given the observed data, so why not choose the value that "matches" (gives the greatest likelihood) to the observed data.
Example: say X1, ..,Xn are iid Ber(p). First notice that a function f has an extremal point at x iff log(f) does as well because
d/dx{log(f(x))}=f'(x)/f(x)=0 iff f'(x)=0
Now
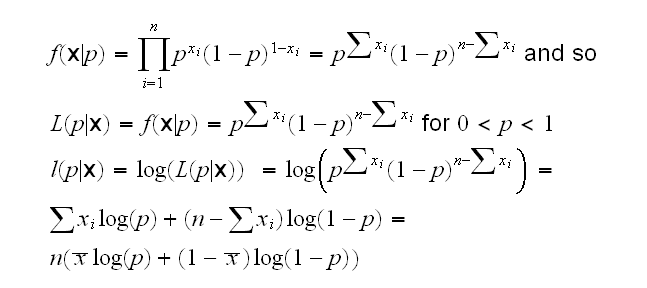
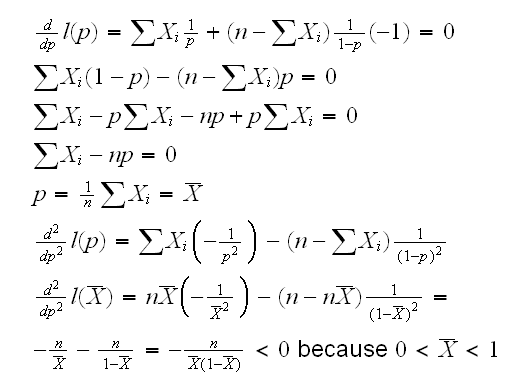
Here we verified that the extrema is really a maxima. Recall that we previously said that the log-likelihood of the normal distribution as a function of μ is a quadratic opening downward, and that because of the central limit theorem the log-likelihood function of many distributions approaches that of a normal. For this reason the log-likelihood function (almost) always has a maximum at the mle. There are exceptions, though:
Example: say X1, ..,Xn are iid U[0,θ], θ>0. Then
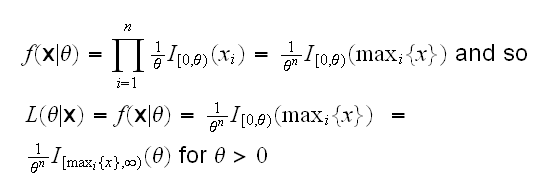
Now L(θ|x) is 0 on (0,max(xi)), at max(xi) it jumps to 1/(max(xi))n and then monotonically decreases as θ gets bigger, so the maximum is obtained at θ=max(xi), therefore the mle is max(xi)
Here is an example: say n=10 and max{xi}=1.55, then the likelihood curve looks like this
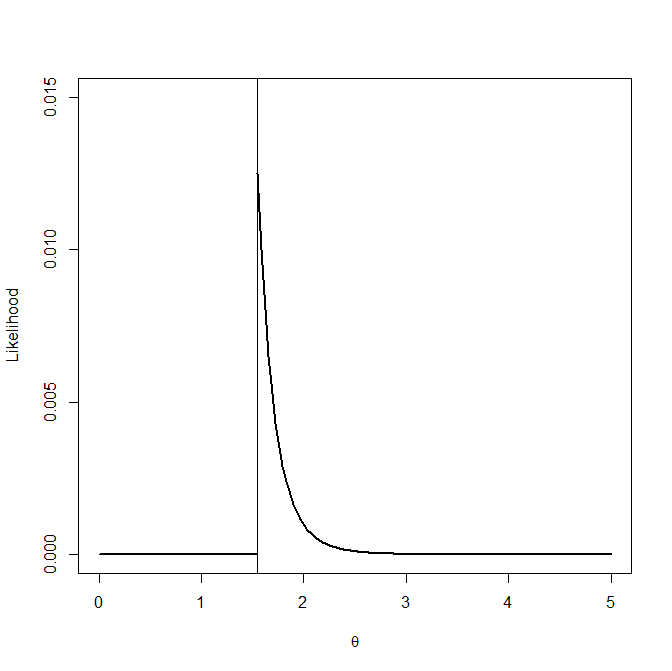
and it has its maximum at 1.55
Notice that here log f is of no use because f(x)=0 for values of x close to the point were the maximum is obtained.
Example X1, .., Xn~N(μ,σ):
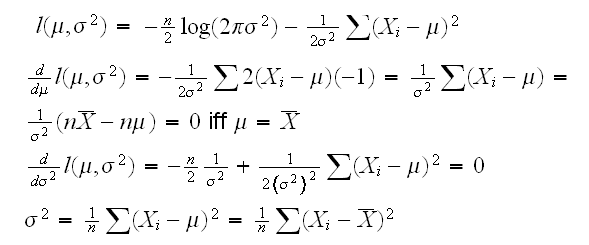
Example say X has a multinomial distribution with parameters p1,..,pk (we assume m is known), then if we simply find the derivatives of the log-likelihood we find
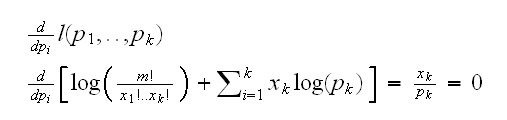
and this system has no solution. The problem is that we are ignoring the condition p1+..+pk=1. So we really have the problem
Minimize l(p1,..,pk) given p1+..+pk=1
One way to do this is with the method of Lagrange multipliers: minimize
l(p1,..,pk)-λ(p1+..+pk-1):
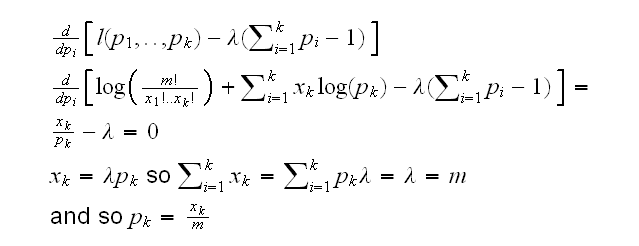
Maximum likelihood estimators have a number of nice properties. One of them is their invariance under transformations. That is if 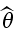 is the mle of θ, then g(
is the mle of θ, then g(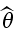 ) is the mle of g(θ)
) is the mle of g(θ)
Example say X1, .., Xn~Ber(p) so we know that the mle isX̅. Say we are interested in θ=p-q=p-(1-p)=2p-1, the difference in proportions. Therefore 2X̅-1 is the mle of θ.
Let's see whether we can verify that. First if θ=2p-1 we have p=(1+θ)/2 and so
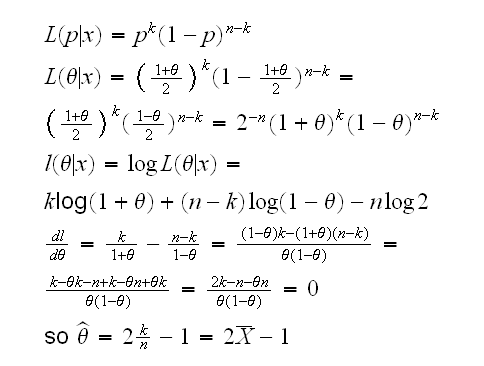
Example say X1, .., Xn~N(μ,σ) so we know that the mle of σ2 is S2 . But then the mle of σ is s.
Definition
Let X=(X1,..,Xn) be a random sample from some pmf (pdf) f(.,θ). Then the quantity
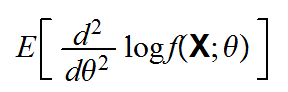
is called the Fisher information number of the sample.
If the sample is identitically distributied things simplify:
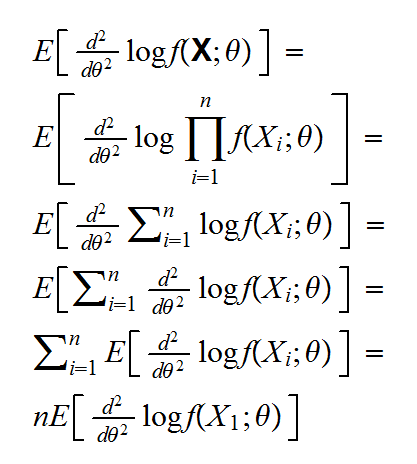
We said before that often the log-likelihood the log-likelihood function of many distributions approaches that of a normal. We can now make this statement precise:
Theorem Let X1, .., Xn be iid f(x|θ). Let 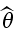 denote the mle of θ. Under some regularity conditions on f we have
denote the mle of θ. Under some regularity conditions on f we have
√n[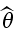 -θ]→N(0,√-v)
-θ]→N(0,√-v)
where v is the Fisher information number
Example say X1, .., Xn are iid Ber(p) and we want to estimate p. We saw above that the mle is given by X̅ .
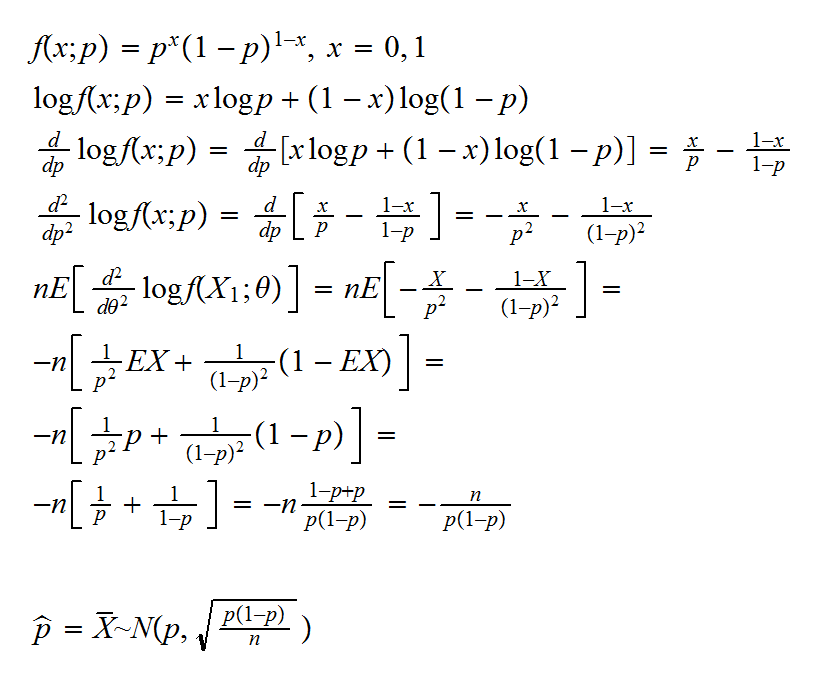
Example say Xi~Exp(λ), i=1,2,.. and the Xi are independent. Then we saw before that if Sn=(X1+..+Xn)
l(λ;x) = nlog(λ)-λSn .
Now
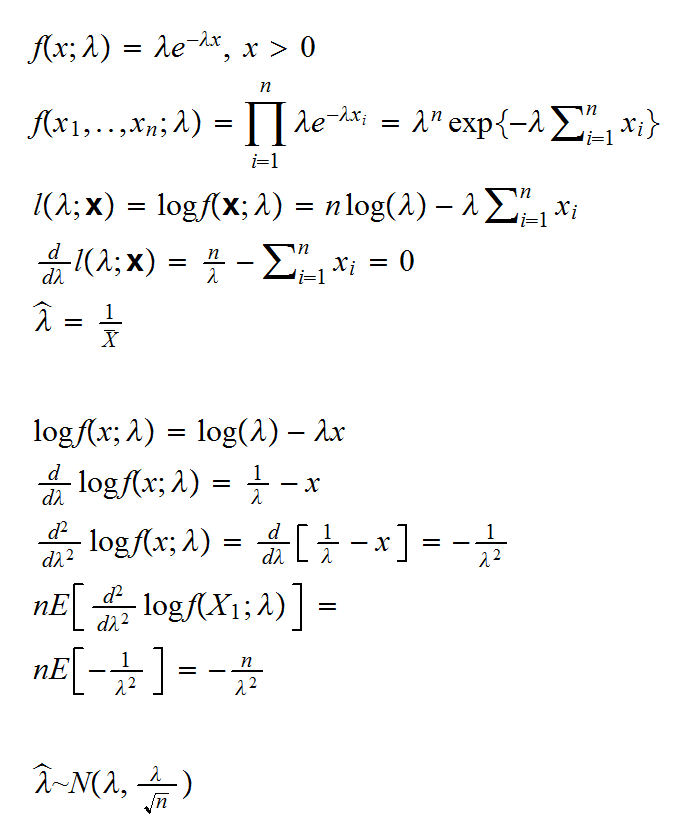
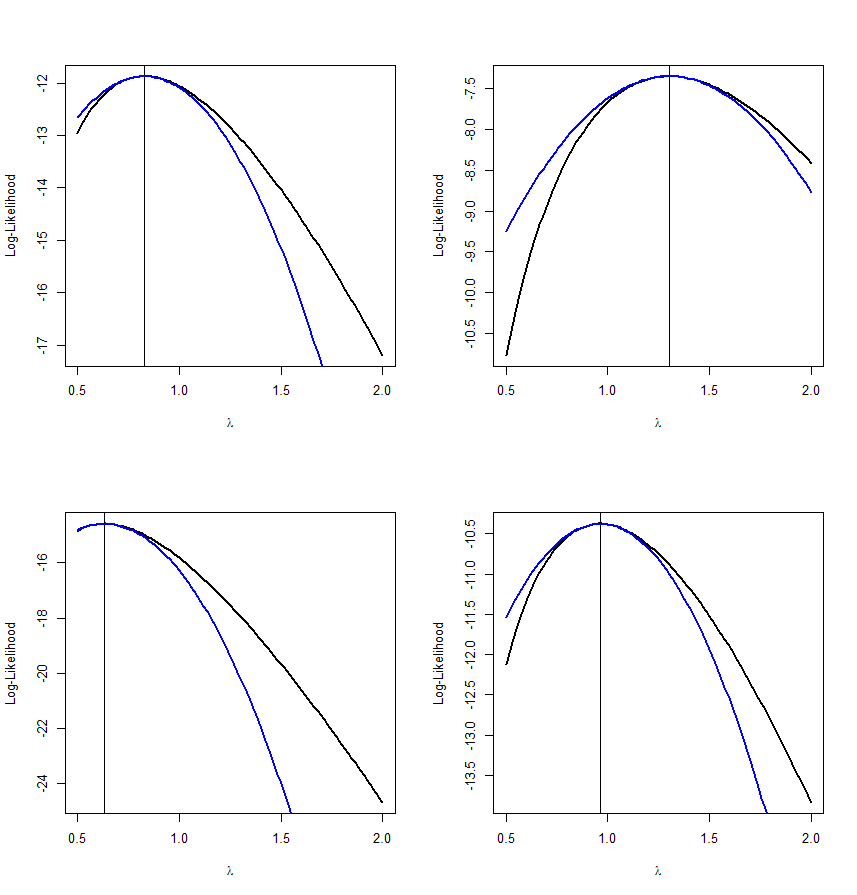
here are 4 examples. n=10, λ=1. The true log-likelihood curve is in black and the parabola from the normal approximation is in blue.
We have already seen how to use a Bayesian approach to do finding point estimators, namely using the mean of the posterior distribution. Of course one could also use the median or any other measure of central tendency. A popular choice for example is the mode of the posterior distribution.
Example Let's say we have X1, .., Xn~Ber(p) and p~Beta(α,β), then we already know that
p|x1,..xn~Beta(α+∑xi,n-∑xi+β)
and so we can estimate p as follows:
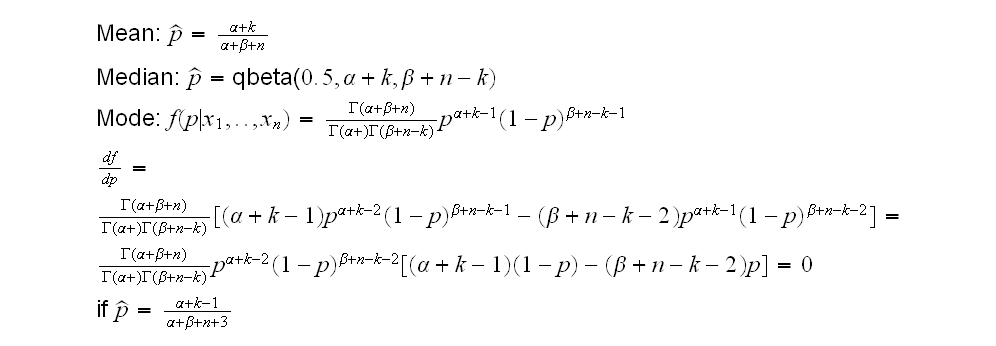
Example: A switch board keeps track of the number of phone calls they receive per hour during the day:
1 5 4 4 3 1 5 5 5 6 7 5 4 4 4 2 4 7 0 3 4 9 4 2
Let's say they believe that the number of calls has a Poisson distribution with rate λ.
a) find the maximum likelihood estimator of the rate λ
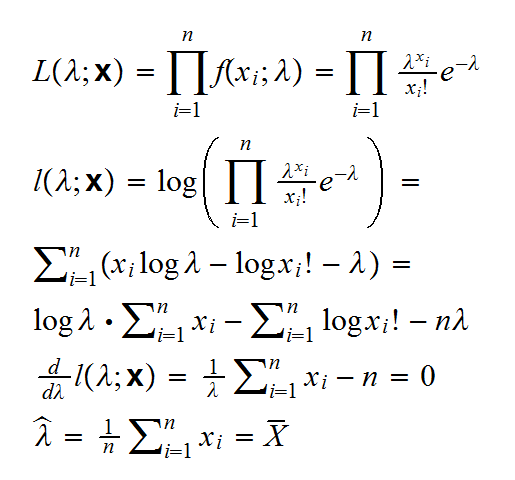
and we find X̅ = 4.08
b) Find the Bayes estimator for λ as the median of the posterior distribution . Use as a prior π(λ)=1/λ, λ>0
This is of course an improper prior because ∫π(λ)dλ=∞
Now

and we get the same answer!