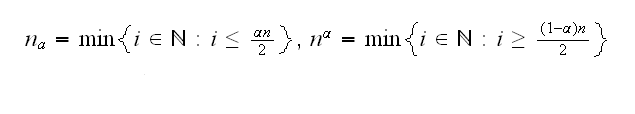The Bootstrap
Example say we have rv's X, Y where X,Y~N(0,1), X Y, and we are interested in estimating the third quartile of X/Y, that is the number q such P(X/Y≤q)=0.75 (it can be shown that q=1.0). So what can we do? Clearly we can generate X1, .., Xn, Y1, .., Yn iid N(0,1), calculate Zi=Xi/Yi and find the 75th sample quantile of the Zi's. This is done in ratio.boot. But how can we get a CI for q? Clearly the Zi are not normal.
Y, and we are interested in estimating the third quartile of X/Y, that is the number q such P(X/Y≤q)=0.75 (it can be shown that q=1.0). So what can we do? Clearly we can generate X1, .., Xn, Y1, .., Yn iid N(0,1), calculate Zi=Xi/Yi and find the 75th sample quantile of the Zi's. This is done in ratio.boot. But how can we get a CI for q? Clearly the Zi are not normal.
Instead we can use a method called the statistical bootstrap. It starts of very strangely: instead of sampling from a distribution as in a standard Monte Carlo study, we will now resample the data itself, that is if the data is n observations X 1, .., X n, then the bootstrap sample is also n numbers with replacement from X1, .., Xn, that is X*1 is any of the original X1, .., Xn with probability 1/n. In any one bootstrap sample an original observation, say X1, may appear once, several times, or not at all.
Example say the data is (5.1, 2.3, 6.4, 7.8, 4.6), then one possible bootstrap sample is (6.4, 4.6, 2.3, 6.4, 5.1)
Say we have a sample X1, .., Xn from some unknown distribution F and we wish to estimate some parameter θ = t(F). For this we find some estimate 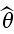 = s(x). How accurate is
= s(x). How accurate is 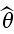 ?
?
Example X1, .., Xn~F, θ = E(X1) so t(F)=∫xf(x)dx and s(x)=X̅
Example X1, .., Xn~F, θ = Var(X1) so t(F)=∫(x-μ)2f(x)dx and s(x)=1/(n-1)∑(Xi-X̅)2
Here is the algorithm to find the bootstrap estimate of the standard error in 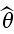 :
:
1) Select B independent bootstrap samples x*1, .., x*B, each consisting of n data values drawn with replacement from x. Here B is usually on the order 100.
2) Evaluate the bootstrap replication corresponding to each bootstrap sample, 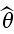 *(b) = s(x*b), b=1,..,B
*(b) = s(x*b), b=1,..,B
3) Estimate the standard error sef(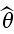 ) by the sample standard deviation of the bootstrap replications.
) by the sample standard deviation of the bootstrap replications.
Example say the data is (5.1, 2.3, 6.4, 7.8, 4.6) and we want to estimate the mean μ, then
1) bootstrap sample 1: x*1= (6.4, 4.6, 2.3, 6.4, 5.1) , so 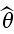 *(1) = s(x*1)=(6.4+4.6+2.3+6.4+5.1)/5=4.96
*(1) = s(x*1)=(6.4+4.6+2.3+6.4+5.1)/5=4.96
2) bootstrap sample 2: x*2= (2.3, 6.4, 4.6, 2.3,7.8) , so 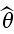 *(2) = s(x*2)=(2.3+6.4+4.6+2.3+7.8)/5=4.68
*(2) = s(x*2)=(2.3+6.4+4.6+2.3+7.8)/5=4.68
and so on
I wrote the function bootstrap to carry out steps 1 and 2. So for our problem we can calculate the bootstrap estimates with the command Q3star=bootstrap(Z,f=quantile, probs=0.75)
Example Let's go back to the example above. Here we have Z1,..,Zn~F where F is the distribution of the ratio of two standard normal rv's, that if X,Y iid N(0,1) F(x)=P(X/Y<x).
We are interested in the third quartile of this distribution, that is the solution of the equation F(x)=0.75. If we denote this number by Q3 we have Q3=inf{x:F(x)≥0.75}=t(F).
After generating the data we have observations Z1,..,Zn, and we can find the third quartile of the data using Q3_est=quantile(Z,0.75)=s(z).
To do the bootstrap we first find a bootstrap sample, find it's third sample quartile, and call the result Q3star1. Now repeat the above about 100 times. Finally we find the bootstrap standard error estimate as the standard error of Q3star1,..Q3star100. The CI is then given by
Q3_est±zα/2sd(Q3star)
Note there is no √n because sd(Q3star) is already the standard error of the estimate, not of the original data.
This is implemented in sb2, which also shows that the bootstrap estimates are indeed normal, which is quite often the case. If they are not we could use a CI based on percentiles as follows: let Q3star[1],.., Q3star[n] be the order statistic of Q3star1,.., Q3starn, that is Q3star1,.., Q3starn ordered from smallest to largest. Let
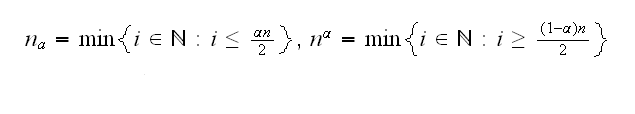
then the nα'th and the nαth order statistic of Q3star is a 100(1-α) CI. nα and nα are called the floor and the ceiling, by the way.
This again is implemented in sb2
How do the normal theory intervals and the percentile intervals perform? This is studied in ratio1.boot were we see that the true coverage (89.0% and 88.8%) of both methods is just about the nominal one.
This idea of the bootstrap is very strange: at first it seems we are getting more out of the data than we should. It is also a fairly new idea, invented by Bradley Efron in the 1980's. Here is some justification why it works:
Let's say we have X1, .., Xn iid F for some cdf F, and we want to investigate the properties of some parameter θ of F, for example its mean or its median. We have an estimator of θ, say s(X1, .., Xn), for example s(X1, .., Xn)=X̅ in the case of the mean. What is the error in s(X1, .., Xn)? In the case of the mean this is very easy and we already know that the answer is sd(X1, .., Xn)/√n. But what if we don't know it and we want to use Monte Carlo simulation to find out? Formally what this means is the following:
Step 1) generate X'1, .., X'n iid F
Step 2) find the θ'=s(X'1, .., X'n)
Step 3) repeat Step 1 and Step 2 many times (say 1000 times)
Step 4) Study the MC estimates of θ, for example find their standard deviation.
But what do we do if we don't know that our sample came from F? A simple idea then is to replace sampling from the actual distribution function by sampling from the next best thing, the empirical distribution function. So the idea of the bootstrap is simple: replace F in the simulation above with Fhat:
Step 1) generate X*1, .., X*n from the empirical distribution function of X1, .., Xn
Step 2) find the estimate s( X*1, .., X*n)
Step 3) repeat Step 1 and Step 2 many times.
Step 4) Study the MC samples s( X*1, .., X*n), for example find their standard deviation.
What does it mean, generate X*1, .., X*n from the empirical distribution function of X1, .., Xn?Actually it means finding a bootstrap sample as described above.
Example : Let's illustrate these ideas using an example from a very good book on the bootstrap, "An Introduction to the Bootstrap" by Bradley Efron and Robert Tibshirani. The following table shows the results of a small experiment, in which 7 out of 16 mice were randomly selected to receive a new medical treatment, while the remaining 9 mice were assigned to the control group. The treatment was intended to prolong survival after surgery. The table shows the survival times in days:
| Treatment |
Control |
| 94 197 16 38 |
52 104 146 10 |
| 99 141 23 |
50 31 40 27 46 |
The data is also in R as mice
How can we answer the question on whether this new treatment is effective? First of course we can find the within group means and standard deviations:
|
Treatment |
Control |
| Mean |
86.86 |
56.22 |
| Standard Deviation |
25.24 |
14.14 |
(with lapply(mice,mean) and lapply(mice,sd) ), so we see that the mice who received the treatment lived on average 30.63 days longer. But unfortunately the standard error of the difference is 28.93 = √(25.242+14.142), so we see that the observed difference 30.63 is only 30.63/28.93 = 1.05 standard deviations above 0.
Let's say next that instead of using the mean we wish to use the median to measure average survival. We find the following:
|
Treatment |
Control |
| Median |
94 |
46 |
| Standard Error |
? |
? |
Now we get a difference in median survival time of 48 days, but what is the standard error of this estimate? Of course there is a formula for the standard error of the median, but it is not simple and just finding it in a textbook would be some work. On the other hand we can use the bootstrap method to find it very easily. It is done in mice.boot, and we find that the standard error of the median in the treatment group is about 37, and for the control group it is about 11, so the standard error of the difference is √(372+112)=38.6, and so 48/38.6=1.25. This is larger than the one for the mean, but still not statistically significant.
Example How good is this bootstrap method, that is how well does it calculate the standard error? Let's investigate this using a situation where we know the right answer:
Say we have n observations from N(μ,σ), then of course sd(X̅)=σ/√n. In bootex we use both the direct estimate of σ and the bootstrap estimator.
 Y, and we are interested in estimating the third quartile of X/Y, that is the number q such P(X/Y≤q)=0.75 (it can be shown that q=1.0). So what can we do? Clearly we can generate X1, .., Xn, Y1, .., Yn iid N(0,1), calculate Zi=Xi/Yi and find the 75th sample quantile of the Zi's. This is done in ratio.boot. But how can we get a CI for q? Clearly the Zi are not normal.
Y, and we are interested in estimating the third quartile of X/Y, that is the number q such P(X/Y≤q)=0.75 (it can be shown that q=1.0). So what can we do? Clearly we can generate X1, .., Xn, Y1, .., Yn iid N(0,1), calculate Zi=Xi/Yi and find the 75th sample quantile of the Zi's. This is done in ratio.boot. But how can we get a CI for q? Clearly the Zi are not normal.
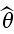 = s(x). How accurate is
= s(x). How accurate is